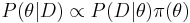Approximate Bayesian computation

Approximate Bayesian computation (ABC) is a family of computational techniques in Bayesian statistics. These simulation techniques operate on summary data (such as population mean, or variance) to make broad inferences with less computation than might be required if all available data were analyzed in detail. They are especially useful in situations where evaluation of the likelihood is computationally prohibitive, or whenever suitable likelihoods are not available.

ABC methods originated in population and evolutionary genetics [1][2] but have recently also been introduced to the analysis of complex and stochastic dynamical systems.[3]

Contents

Overview

In standard Bayesian inference the posterior distribution is given by

P(\theta|D)\propto P(D|\theta) \pi(\theta)

where \theta are the parameters of a probability model, D are the observed data, and 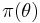\pi(\theta) is the prior distribution of the parameters 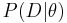\theta. P(D|\theta) is the likelihood of \theta, that is the probability of observing the data D given the model with parameter \theta.

The explicit evaluation of the likelihood 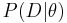P(D|\theta) is avoided in ABC approaches by considering distances between observed and data simulated from a model with parameter \theta. For sufficiently complex models and large data sets the probability of happening upon a simulation run that yields precisely the same dataset as the one observed will be very small, often unacceptably so. So rather than considering the data we consider a summary statistic of the data, 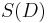S(D), and use a distance 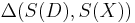\Delta(S(D),S(X)) between the summary statistics of real and simulated data, D and X, respectively.

The generic ABC approach to infer the posterior probability distribution of a parameter \theta is as follows:

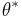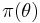  1. Sample a candidate parameter vector \theta^\ast from some proposal distribution \pi(\theta).
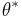  2. Simulate a dataset X from the model with parameter \theta^\ast.
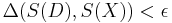  3. If \Delta(S(D),S(X))<\epsilon then accept 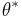\theta^\ast as a sample from the posterior.

For \epsilon sufficiently small the ABC procedure should deliver a good approximation to the true posterior, in particular if the summary statistic S is a sufficient statistic of the probability model. If sufficient statistics do not exist or are hard to come by, setting up a satisfying and efficient ABC approach can be challenging.

The generic procedure outlined above can be computationally inefficient but ABC and likelihood-free inferential procedures can be combined with the standard computational approaches used in Bayesian inference such as Markov chain Monte Carlo [4][5] and Sequential Monte Carlo method [3] approaches. In these frameworks ABC can be used to tackle otherwise computationally intractable problems.

While ABC and related likelihood-free methods have overwhelmingly been employed for parameter estimation, they can also be used for model selection, as the whole apparatus of Bayesian model selection can be adapted to the ABC framework.[6]

An increasing number of software implementations of ABC approaches exist.[7][8][9]

Recent advances in ABC methodology, computational implementations and applications are discussed at the ABC in ... meetings:

See also

References

  1. ^ Pritchard, J. K.; Seielstad, M. T., Perez-Lezaun, A., and Feldman, M. T. (1999). "Population Growth of Human Y Chromosomes: A Study of Y Chromosome Microsatellites". Mol. Biol. Evol. 16 (12): 1791–1798. PMID 10605120. 
  2. ^ Beaumont, M. A.; Zhang, W. and Balding, D. J. (December 1, 2002). "Approximate Bayesian computation in population genetics". Genetics 162 (4): 2025–2035. PMC 1462356. PMID 12524368. http://www.genetics.org/cgi/content/abstract/162/4/2025. 
  3. ^ a b Toni, T.; Welch, D.; Strelkowa, N.; Ipsen, A.; Stumpf, M.P.H. (2009). "Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems". Journal of the Royal Society Interface 6 (31): 187–202. doi:10.1098/rsif.2008.0172. http://rsif.royalsocietypublishing.org/content/6/31/187.abstract. 
  4. ^ Marjoram, P.; Molitor, J., Plagnol, V. and Tavaré, S. (2003). "Markov chain Monte Carlo without likelihoods". P Natl Acad Sci USA 100 (26): 15324–15328. doi:10.1073/pnas.0306899100. PMC 307566. PMID 14663152. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=307566. 
  5. ^ Plagnol, V.; Tavaré, S. (2004). "Approximate Bayesian computation and MCMC" (PDF). Monte Carlo and Quasi-Monte Carlo Methods 2002. http://www-gene.cimr.cam.ac.uk/vplagnol/papers/vpst-web.pdf.  (The link is to a preprint.)
  6. ^ Toni, T.; Stumpf, M.P.H. (2010). "Simulation-based model selection for dynamical systems in systems and population biology" (PDF). Bioinformatics 26 (1): 104–10. doi:10.1093/bioinformatics/btp619. PMC 2796821. PMID 19880371. http://bioinformatics.oxfordjournals.org/cgi/reprint/26/1/104.pdf. 
  7. ^ Cornuet, J-M.; Santos, F., Beaumont, M. A., Robert, C. P., Marin, J-M., Balding, D. J., Guillemaud, T. and Estoup, A. (2008). "Inferring population history with DIY ABC: a user-friendly approach to approximate Bayesian computation". Bioinformatics 24 (23): 2713–9. doi:10.1093/bioinformatics/btn514. PMC 2639274. PMID 18842597. http://bioinformatics.oxfordjournals.org/cgi/content/abstract/btn514. 
  8. ^ Liepe, J.; Barnes, C.; Cule, E.; Erguler, K.; Kirk, P.; Toni, T.; Stumpf, M.P.H. (2010). "ABC-SysBio—approximate Bayesian computation in Python with GPU support". Bioinformatics 26 (14): 1797–9. doi:10.1093/bioinformatics/btq278. PMC 2894518. PMID 20591907. http://bioinformatics.oxfordjournals.org/cgi/content/full/26/14/1797. 
  9. ^ Wegmann, D.; Leuenberger, C.; Neuenschwander, S.; Excoffier, L. (2010). "ABCtoolbox: a versatile toolkit for approximate Bayesian computations". BMC Bioinformatics 11: 116. doi:10.1186/1471-2105-11-116. PMC 2848233. PMID 20202215. http://www.biomedcentral.com/1471-2105/11/116. 

Software

DIYABC : "Do it yourself ABC".

ABC SysBio : A Tool for parameter inference and model selection in systems biology (see also Theoretical Background).

ABC Toolbox: Inference for Population Genetics.

msBayes : Comparative phylogeographic inference